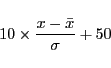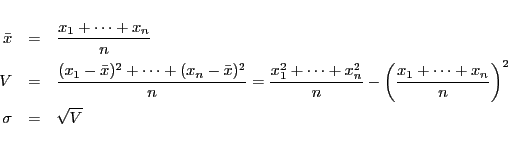

Next: 注意
Up: 情報科学演習 第11回 表計算ソフトを用いた統計処理
Previous: 本日の目標
としひこ, せいこ, まさひこ, なおこ, いよ, よしおの6人が
ある試験でそれぞれ, 3点, 4点, 8点, 10点, 7点, 5点を取ったとします.
これらのデータをもとに, 平均点と各人の偏差値を計算します.
偏差値は, 素点を 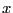 とすると,
標準偏差
とすると,
標準偏差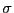 と平均
と平均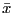 を使って次の式で定義されます.
を使って次の式で定義されます.
標準偏差は, 偏差(平均値からの偏り)の平均です.
正確には次のように, 分散の平方根として定義されます:
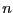 人の人の点数が,
人の人の点数が,
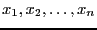 とし, 平均を
とし, 平均を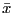 ,
分散を
,
分散を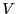 , 標準偏差を
, 標準偏差を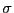 とすると,
とすると,
となります. 分散の式の 2番目の等式は簡単に証明できるので,
証明してみて下さい.
なお, 偏差値は受験用語で数学用語ではありません
(純粋に日本語で, 例えば英語に対応する言葉はありません.
deviation valueと直訳すると違う意味になります.)が,
分散,標準偏差は, 医学や工学など実験系はもちろん,
経済学, 社会学, 教育学などデータ分析をするときには
必要とされる基本用語です.
定義も簡単なので, この機会に覚えて下さい.
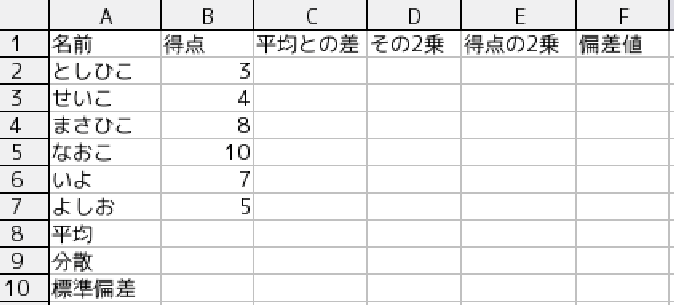
次の指示に従い, 図1の表を完成させます.
- 図1にあるデータおよび項目名を入力して下さい.
- 次に, 関数AVERAGEを使用して, セルB8に 6人の成績の平均値を計算する
式を書きます.
- C2に「としひこ」の得点(B2)と6人の平均点(B8)の差を
式で入力します.
この時,「=B2-B8」と入力してしまうと,
C3にこの式をコピーした時に「=B3-B9」が入力され,
本来求める値とは異なる計算結果になります.
(このようなセルの参照を「相対参照」といいます.)
これに対して, 平均点の記述されたセル(B8)のように
どのセルからもそのセルの値を共通に利用したい場合,
「絶対参照」という方法を用います.
絶対参照をするためには, セルの行番号と列のアルファベットの前に,
$を入れます. 例えば, セルB8を絶対参照するためには, $B$8とします.
したがって, C2 に入れる式は, B2-$B$8 となります.
他にも「複合参照」という方法がありますが,
こちらは自習して下さい.
絶対参照とコピー&ペーストを利用して, 表を完成させます.
- C2をコピーしてから C3〜C7 にペーストします
- D2〜D7にはC列の2乗を式で入力します.
- E 列には, B列の 2乗が入るように式を入力します.
- E8には「各人の得点の2乗」の平均を入力します.
(E2〜E7の平均を計算する式を入力.)
- B9に 6人の成績の分散を入力します.
(分散は「2乗の平均-平均の2乗」ですから,
E8からB8の2乗を引いた式を書くことになります.)
- D8にD2〜D7の平均を計算する式を入力します.
(この値は「各人の得点から平均点を引いたもの」の2乗ですから,
分散の定義式です. B9の値と一致することを確認して下さい.)
- B10 に標準偏差を入力します. 平方根を求めるには,
SQRTという関数を利用します.)
- F2〜F7に各人の偏差値を計算する式を入力します.
- C8にC2〜C7の平均を計算する式を書きます.
(この値は,理論上0と表示されるものですが,
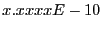 のように表示されることがあります.
これは,
のように表示されることがあります.
これは,
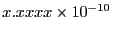 の意味で0に非常に近い値です.
小数の計算においては, 計算機は無限小数や非常に小さい数を
途中で値を四捨五入するため理論値との誤差を生じることがあります.)
の意味で0に非常に近い値です.
小数の計算においては, 計算機は無限小数や非常に小さい数を
途中で値を四捨五入するため理論値との誤差を生じることがあります.)
Subsections


Next: 注意
Up: 情報科学演習 第11回 表計算ソフトを用いた統計処理
Previous: 本日の目標
2008-07-07


![]() とすると,
標準偏差
とすると,
標準偏差![]() と平均
と平均![]() を使って次の式で定義されます.
を使って次の式で定義されます.