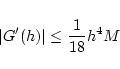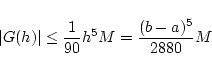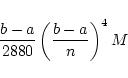Next: 例
Up: 計算機言語I 第9回 数値積分 台形公式とシンプソンの公式
Previous: シンプソンの公式
シンプソンの公式は, 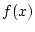 が良い性質をもつ時, 台形公式より
正確な近似値を与える事が知られています.
が良い性質をもつ時, 台形公式より
正確な近似値を与える事が知られています.
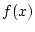 を 4 階連続微分可能な関数とし,
を 4 階連続微分可能な関数とし, 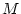 を
を 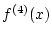 の
閉区間
の
閉区間 ![$[a,b]$](img2.png) での最大値とします.
での最大値とします.
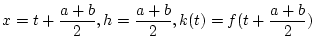 とおきます. 積分値と近似値の誤差を
とおきます. 積分値と近似値の誤差を 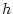 の関数と見て
の関数と見て
とおきます. 上の式の 3 階微分を計算する事により,
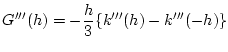 |
|
|
(5) |
が成立します. ここで平均値の定理より 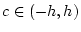 が存在して,
が存在して,
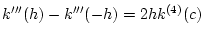 となります.
また,
となります.
また,
ですから
で, 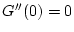 より,
より,
同様に 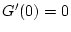 で上と同じような積分計算をすると,
で上と同じような積分計算をすると,
となり, さらにもう一度積分して誤差の評価は
を得ます. したがって区間を 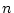 等分した時の近似値と積分値の誤差は
等分した時の近似値と積分値の誤差は
で押さえられます.
Subsections
Next: 例
Up: 計算機言語I 第9回 数値積分 台形公式とシンプソンの公式
Previous: シンプソンの公式
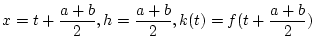 とおきます. 積分値と近似値の誤差を
とおきます. 積分値と近似値の誤差を ![]() を 4 階連続微分可能な関数とし,
を 4 階連続微分可能な関数とし, ![]() を
を ![]() の
閉区間
の
閉区間 ![]() での最大値とします.
での最大値とします.
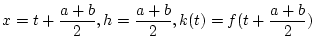 とおきます. 積分値と近似値の誤差を
とおきます. 積分値と近似値の誤差を ![]() の関数と見て
の関数と見て
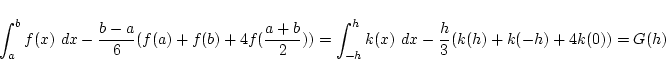
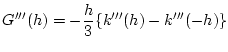
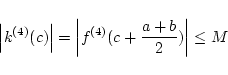
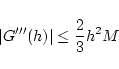
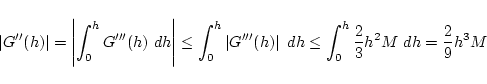
![]() で上と同じような積分計算をすると,
で上と同じような積分計算をすると,