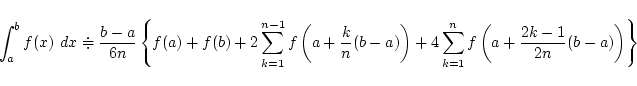Next: シンプソンの公式の誤差
Up: 計算機言語I 第9回 数値積分 台形公式とシンプソンの公式
Previous: 例: 台形公式による定積分の数値計算
まず, 簡単のために区間を分割しない場合を考えます.
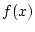 を閉区間
を閉区間 ![$[a,b]$](img2.png) 上の連続関数とします. 台形公式は,
これを 1 次関数で近似して積分を計算するのに対し, シンプソンの公式は
2 次関数で近似します. 2 次関数のグラフは 3 点の値で決定されますが,
それらは,
上の連続関数とします. 台形公式は,
これを 1 次関数で近似して積分を計算するのに対し, シンプソンの公式は
2 次関数で近似します. 2 次関数のグラフは 3 点の値で決定されますが,
それらは,
![$[a, f(a)], [(a+b)/2, f((a+b)/2)], [b, f(b)]$](img48.png) です.
即ち, この 3 点を通る 2 次関数を
です.
即ち, この 3 点を通る 2 次関数を 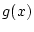 とする時,
とする時, 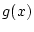 の積分
の値を
の積分
の値を 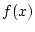 の積分の近似値だと思います.
の積分の近似値だと思います.
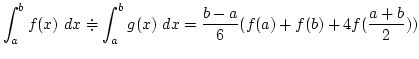 |
|
|
(4) |
区間 ![$[a,b]$](img2.png) を
を 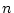 等分した場合, 上の近似値は次のようになります.
等分した場合, 上の近似値は次のようになります.
Next: シンプソンの公式の誤差
Up: 計算機言語I 第9回 数値積分 台形公式とシンプソンの公式
Previous: 例: 台形公式による定積分の数値計算
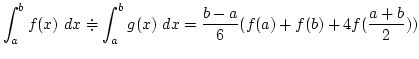
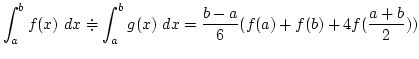
![]() を
を ![]() 等分した場合, 上の近似値は次のようになります.
等分した場合, 上の近似値は次のようになります.