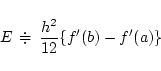Next: 例: 台形公式による定積分の数値計算
Up: 台形公式
Previous: 台形公式
定積分に関する次の部分積分法の式を用いると,
台形公式による数値積分の誤差について調べられる.
![$\displaystyle \int_\alpha^{\beta}h(x)g'(x) dx =
\left[h(x)g(x)\right]_\alpha^\beta-\int_\alpha^{\beta}h'(x)g(x) dx$](img16.png) |
|
|
(1) |
定積分
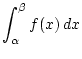 は,
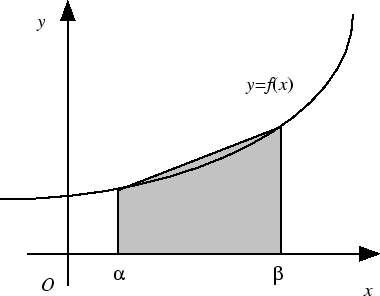
次の図の斜線の面積で近似するとその誤差は, 次のようになる.
は,
次の図の斜線の面積で近似するとその誤差は, 次のようになる.
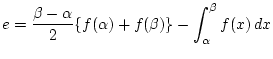 |
|
|
(2) |
部分積分法の公式を用いて, まず次の等式が成り立つことを示そう.
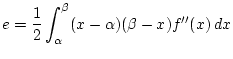 |
|
|
(3) |
公式 (1) において, 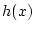 として
として
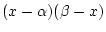 ,
,
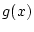 として
として 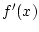 をとると, (3)の右辺は次のようになる.
をとると, (3)の右辺は次のようになる.
再び公式 (1) において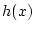 として
として
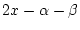 ,
,
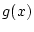 として
として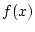 をとると, 上の式は次のようになる.
をとると, 上の式は次のようになる.
これは(2)の右辺に等しいから, (3)の等式が成り立つ.
前節において, 定積分
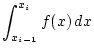 を
を
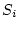 で近似したときの誤差は
で近似したときの誤差は
これは,公式の (2) で
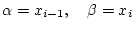 とおいた式であるから
(3) により
とおいた式であるから
(3) により
ここで
であるから, 小区間
![$[x_{i-1}, x_i]$](img34.png) において,
において, 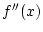 の最大値を
の最大値を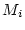 ,
最小値を
,
最小値を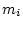 とすると, 次の公式が成り立つ.
とすると, 次の公式が成り立つ.
関数 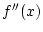 が連続であるとき, 分割の個数
が連続であるとき, 分割の個数 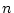 を大きくとって, 小
区間の幅
を大きくとって, 小
区間の幅 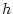 を小さくすると
を小さくすると
となる. よって, 定積分
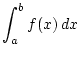 の台形公式
による近似値の誤差は
の台形公式
による近似値の誤差は
ここで, 関数 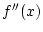 の区分求積法による数値積分を考えると
の区分求積法による数値積分を考えると
ゆえに
従って, 誤差は小区間の幅の平方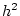 にほぼ比例し,
にほぼ比例し,
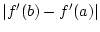 が小さければ, 誤差も小さいことがわかる.
が小さければ, 誤差も小さいことがわかる.
Next: 例: 台形公式による定積分の数値計算
Up: 台形公式
Previous: 台形公式
![$\displaystyle \int_\alpha^{\beta}h(x)g'(x) dx =
\left[h(x)g(x)\right]_\alpha^\beta-\int_\alpha^{\beta}h'(x)g(x) dx$](img16.png)
![$\displaystyle \int_\alpha^{\beta}h(x)g'(x) dx =
\left[h(x)g(x)\right]_\alpha^\beta-\int_\alpha^{\beta}h'(x)g(x) dx$](img16.png)
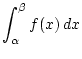 は,
次の図の斜線の面積で近似するとその誤差は, 次のようになる.
は,
次の図の斜線の面積で近似するとその誤差は, 次のようになる.
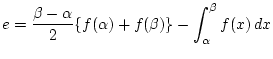
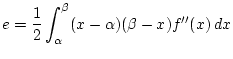

![]() として
として
![]() ,
,
![]() として
として ![]() をとると, (3)の右辺は次のようになる.
をとると, (3)の右辺は次のようになる.
![\begin{displaymath}\frac{1}{2}{\left[(x-\alpha)(\beta-x)f'(x)\right]_\alpha^\bet...
... = \frac{1}{2}\int_{\alpha}^{\beta}(2x-\alpha-\beta)f'(x) dx
\end{displaymath}](img25.png)
![]() として
として
![]() ,
,
![]() として
として![]() をとると, 上の式は次のようになる.
をとると, 上の式は次のようになる.
![\begin{displaymath}\frac{1}{2}\left[(2x-\alpha-\beta)f(x)\right]_\alpha^{\beta}-
\int_\alpha^{\beta}f(x) dx \end{displaymath}](img28.png)
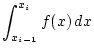 を
を
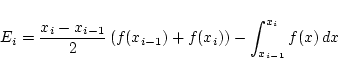
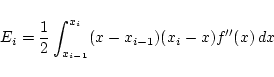
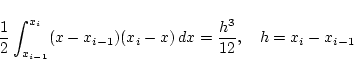
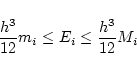
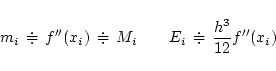
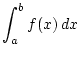 の台形公式
による近似値の誤差は
の台形公式
による近似値の誤差は
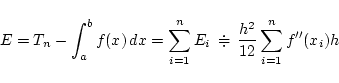
![\begin{displaymath}\sum_{i=1}^{n}f''(x_i)h = \int_{a}^{b}f''(x) dx=[f'(x)]_{a}^{b}=
f'(b)-f'(a)\end{displaymath}](img42.png)