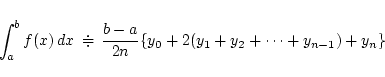Next: 台形公式と誤差
Up: 計算機言語I 第9回 数値積分 台形公式とシンプソンの公式
Previous: 計算機言語I 第9回 数値積分 台形公式とシンプソンの公式
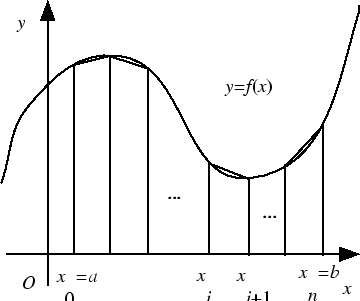
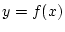 を連続函数とします.図の様に区間
を連続函数とします.図の様に区間![$[a,b]$](img2.png) を
を 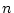 等分して,
分点を順に
等分して,
分点を順に
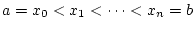 とし,
とし,
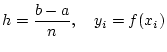 とする.
とする.
小区間![$[x_{i-1},x_i]$](img7.png) で, 区間の幅
で, 区間の幅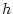 を高さとし,
を高さとし, 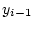 と
と
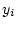 を各々上底, 下底とする台形の面積を
を各々上底, 下底とする台形の面積を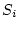 とすると
とすると
これらの台形の面積の総和を
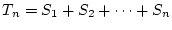 とすると
これは,
とすると
これは, 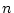 が十分に大きいと,
定積分
が十分に大きいと,
定積分
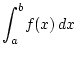 の近似値を与える.
従って, 定積分の近似式を与える次の 台形公式 が得られる.
の近似値を与える.
従って, 定積分の近似式を与える次の 台形公式 が得られる.
Subsections
Next: 台形公式と誤差
Up: 計算機言語I 第9回 数値積分 台形公式とシンプソンの公式
Previous: 計算機言語I 第9回 数値積分 台形公式とシンプソンの公式
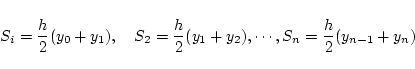
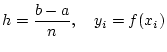 とする.
とする.

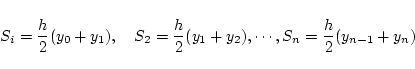
![]() とすると
これは,
とすると
これは, ![]() が十分に大きいと,
定積分
が十分に大きいと,
定積分
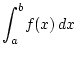 の近似値を与える.
従って, 定積分の近似式を与える次の 台形公式 が得られる.
の近似値を与える.
従って, 定積分の近似式を与える次の 台形公式 が得られる.