ニュートン法から現れるフラクタル

前回講義したニュートン法は虚数解の数値計算にも使えるか, と いう問題を考えてみます.

少し考えれば分かるように, 以前述べた 2 分法は実数の持つ順序構造に 深く依存しています. 実数解の計算には, 2 分法はとても有効ですが, 自然な順序構造を持たない複素数解の計算には全く役に立ちません.

ニュートン法は, その計算の形から複素数の計算としてとらえる事ができます. また, ニュートン法から決まる数列の極限は, 存在すれば $f(x)=0$ の解 になることは, 実数であろうと複素数であろうと同じです. では, 解の近似計算に対してどの程度有効な方法であるかですが, この問題は 19世紀から考えられて来ました. 結論を 言うと, 実はとても難しい問題であり, その難しさが明らかになったのは, コンピュータが発達して数値計算が高速にできるようになった, ここ 30 年程の出来事です.

まず第 1の難しさは, 中間値の定理がうまく機能しない点にあります. すなわち, 複素数解の場合, 解の存在する範囲を確定するのが実数解程 単純ではないわけです.

第 2の難しさは, 実際に計算を実行する事により分かるのですが, どの解にどの程度の速さで収束するのかの予想がとても困難である事が, 分かった事です. 初期値によって収束先の変化が敏感に変化する いわゆるカオスと呼ばる現象が現れます. ただし, 今世紀になってから 初期値を上手に選べば全ての解が得られる事が証明されたようです.

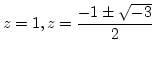ここでは, このカオスの様子をグラフィックスにしてみます. 考える方程式は 1の 3乗根, 即ち $z^3 -1 = 0$ の解を考えます. この方程式の解は, $${z=1, z=\frac{-1\pm\sqrt{-3}}{2}}$$ ですが, 初期値によってこれらの収束先によって, RGB (Red, Green, Blue: 色の三原色)で色分けされた グラフィックスファイルを作ります.