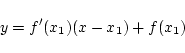
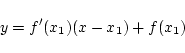
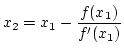 |
(1) |
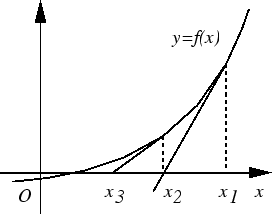
次に, 点![]() における曲線の接線と
における曲線の接線と
![]() 軸との交点の
軸との交点の![]() 座標を
座標を![]() とし, この操作を繰り返すと, 数列
とし, この操作を繰り返すと, 数列
| (2) |
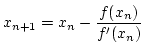 |
(3) |
ニュートン法では, 2分法と違って, 誤差の限界の正確な判定ができません.
ここでは, 数列 (2) において,
![]() となったとき,
となったとき, ![]() は誤差の限界が
は誤差の限界が![]() の近似解であると考えます.
の近似解であると考えます.
誤差の限界を ![]() として, 方程式
として, 方程式 ![]() の近似解を
ニュートン法で求める手順は, 次のようになります.
の近似解を
ニュートン法で求める手順は, 次のようになります.
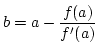 を求める.
を求める.
次の例は, ![]() の唯一の実数解の近似値をニュートン法で
求めるプログラムです. 手抜きをして, 絶対誤差を評価したプログラムです.
の唯一の実数解の近似値をニュートン法で
求めるプログラムです. 手抜きをして, 絶対誤差を評価したプログラムです.
/* File name 7-3.c */
#include <stdio.h>
#include <math.h>
#define EPSILON 1.0E-10
double next(double x);
main()
{
double ans, ans1;
ans=0.0;
ans1=next(ans);
while (fabs(ans-ans1) > EPSILON){
ans1=ans;
ans=next(ans1);
}
printf("%1.10f\n", ans);
}
double next(double x)
{
return (x-(x*x*x+x+1)/(3*x*x+1));
}