


Next: 配列
Up: 計算機言語 I 第 6
Previous: 整数型の計算
最初の 6-1.c の結果の解説をします.
プログラムでは, a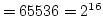 と初期化しています. それを2乗した数,
と初期化しています. それを2乗した数,
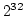 を出力させると, 0 という結果がでます. 皆さんの環境では int型は
32ビットの数です. 32ビットの2進法
を出力させると, 0 という結果がでます. 皆さんの環境では int型は
32ビットの数です. 32ビットの2進法 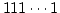 (32桁)は
(32桁)は 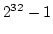 です.
これに 1 を加えると 数学的には
です.
これに 1 を加えると 数学的には 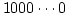 (33桁)となりますが,
皆さんが使っている C言語の整数型は 32ビットなので, 最上位桁の 1は計算の中
で捨てられてしまい, 結果は
(33桁)となりますが,
皆さんが使っている C言語の整数型は 32ビットなので, 最上位桁の 1は計算の中
で捨てられてしまい, 結果は 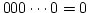 となるのです.
となるのです.
上のことを利用して負の数を実現します. 即ち, 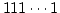 は
1を加えると 0 となる数ですから -1 とするのです. この仕組みで
0 を中心に対称になるように正負の数を扱おうとすると,
次のようになります.
は
1を加えると 0 となる数ですから -1 とするのです. この仕組みで
0 を中心に対称になるように正負の数を扱おうとすると,
次のようになります.
- 非負の数は
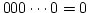 から
から
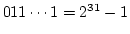 までの数で, 最上位のビットが 0.
までの数で, 最上位のビットが 0.
- 負の数は
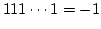 から
から
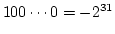 までの数で, 最上位のビットが 1.
までの数で, 最上位のビットが 1.
この形で負の数を実現することを, 『2の補数』表現といいます.
復習の意味で次の問題をやって下さい.
- 問題 1(2進法, 8進法, 16進法)
- 空欄を埋めて下さい.
計算機内部での整数の表記は 2進法を使用しています.
例えば10進法で37は, 2進法では
![\framebox[3em]{ }](img12.png) となります.
2進法で
となります.
2進法で101110と表示された数は,
10進法では,
![\framebox[2em]{ }](img13.png) となります.
2進法を 8進法や16進法に変換するのは, 8と16が各々,
2の3乗, 4乗であることを利用すると簡単になります.
となります.
2進法を 8進法や16進法に変換するのは, 8と16が各々,
2の3乗, 4乗であることを利用すると簡単になります.
101110の場合, 右から 3桁毎に区切ると,
上位 3桁は,101なので, 8進法で
![\framebox[1em]{ }](img14.png) ,
下位 3桁は,
,
下位 3桁は,110なので, 8進法で
![\framebox[1em]{ }](img14.png) となりますから,
全体を 8進法表示すると
となりますから,
全体を 8進法表示すると
![\framebox[2em]{ }](img13.png) になります.
同じ数を16進法で表示するには, 右から 4桁毎に区切ると
上位 4桁(この場合 2桁)は,
になります.
同じ数を16進法で表示するには, 右から 4桁毎に区切ると
上位 4桁(この場合 2桁)は, 10なので,
![\framebox[1em]{ }](img14.png) ,
下位 4桁は, 1110なので, 10進法で,
,
下位 4桁は, 1110なので, 10進法で,
![\framebox[2em]{ }](img13.png) となります.
16進法では, 9より大きい数を 1桁で表すのに, 順に A, B, ..., F を
用いますから, この数を16進法で表すと
となります.
16進法では, 9より大きい数を 1桁で表すのに, 順に A, B, ..., F を
用いますから, この数を16進法で表すと
![\framebox[1em]{ }](img14.png) となります.
従って, 全体を16進法で表示すると
となります.
従って, 全体を16進法で表示すると
![\framebox[2em]{ }](img13.png) となります.
となります.
- 問題 2(符号なしの表記法)
- 空欄を埋めて下さい.
8ビット符号無整数の最小値は0,最大値は 2進表示で
![\framebox[2em]{ }](img13.png) ,
16進表示で
,
16進表示で
![\framebox[2em]{ }](img13.png) ,10進表示で
,10進表示で
![\framebox[2em]{ }](img13.png) です.
です.
- 問題 3(符号付きの表記法)
- 空欄を埋めて下さい.
符号付きの整数を表す場合, 2進表示の最上位の桁(ビット)によって正負を決めます.
最上位の数字が
![\framebox[1em]{ }](img14.png) の時は正の数で,
の時は正の数で,
![\framebox[1em]{ }](img14.png) の時は
負の数を表します. 負の数を表すのに全てのビットを反転して,
1を加える方法があり, この方法を
の時は
負の数を表します. 負の数を表すのに全てのビットを反転して,
1を加える方法があり, この方法を
![\framebox[4em]{ }](img15.png) 表示といいます.
この方法で, -1を 8ビットの 2進法で表すと次になります.
1は 8ビットの 2進法で
表示といいます.
この方法で, -1を 8ビットの 2進法で表すと次になります.
1は 8ビットの 2進法で00000001ですから, これを反転すると,
![\framebox[4em]{ }](img15.png) , さらに 1を加えると
, さらに 1を加えると
![\framebox[4em]{ }](img15.png) となります.
これは16進法で
となります.
これは16進法で
![\framebox[2em]{ }](img13.png) となります.
同じ方法で10進法の-41を表すと,
+41は 8ビットの 2進法では,
となります.
同じ方法で10進法の-41を表すと,
+41は 8ビットの 2進法では,
![\framebox[4em]{ }](img15.png) ですから,
これを反転すると,
ですから,
これを反転すると,
![\framebox[4em]{ }](img15.png) , さらに 1を加えた,
, さらに 1を加えた,
![\framebox[4em]{ }](img15.png) が, -41の 8ビットの 2進表示となります.
これを16進法で表すと
が, -41の 8ビットの 2進表示となります.
これを16進法で表すと
![\framebox[2em]{ }](img13.png) となります.
となります.
- 問題 4
- 空欄を埋めて下さい.
問題 3の方法による符号付き整数の表示で 8ビットの最大の整数は,
最上位ビットが符号を表すことに注意すると, 2進法で
![\framebox[4em]{ }](img15.png) となります.
これを16進法にすると
となります.
これを16進法にすると
![\framebox[2em]{ }](img13.png) で, 10進法では,
で, 10進法では,
![\framebox[2em]{ }](img13.png) になります.
これの符号を変えたものの 2進表示(反転して 1を加える)は,
になります.
これの符号を変えたものの 2進表示(反転して 1を加える)は,
![\framebox[4em]{ }](img15.png) となります.
最小の整数はこれより 1小さく,
となります.
最小の整数はこれより 1小さく,
![\framebox[4em]{ }](img15.png) となります.
これは16進法では
となります.
これは16進法では
![\framebox[2em]{ }](img13.png) , 10進法では
, 10進法では
![\framebox[2em]{ }](img13.png) です.
16ビットの符号付きの整数の最大値は,
16進法で
です.
16ビットの符号付きの整数の最大値は,
16進法で
![\framebox[4em]{ }](img15.png) , 最小値は, 16進法で
, 最小値は, 16進法で
![\framebox[4em]{ }](img15.png) となります.
10進法ではそれぞれ
となります.
10進法ではそれぞれ
![\framebox[4em]{ }](img15.png) ,
,
![\framebox[4em]{ }](img15.png) となります.
となります.
Next: 配列
Up: 計算機言語 I 第 6
Previous: 整数型の計算
![]() と初期化しています. それを2乗した数,
と初期化しています. それを2乗した数,
![]() を出力させると, 0 という結果がでます. 皆さんの環境では int型は
32ビットの数です. 32ビットの2進法
を出力させると, 0 という結果がでます. 皆さんの環境では int型は
32ビットの数です. 32ビットの2進法 ![]() (32桁)は
(32桁)は ![]() です.
これに 1 を加えると 数学的には
です.
これに 1 を加えると 数学的には ![]() (33桁)となりますが,
皆さんが使っている C言語の整数型は 32ビットなので, 最上位桁の 1は計算の中
で捨てられてしまい, 結果は
(33桁)となりますが,
皆さんが使っている C言語の整数型は 32ビットなので, 最上位桁の 1は計算の中
で捨てられてしまい, 結果は ![]() となるのです.
となるのです.
![]() は
1を加えると 0 となる数ですから -1 とするのです. この仕組みで
0 を中心に対称になるように正負の数を扱おうとすると,
次のようになります.
は
1を加えると 0 となる数ですから -1 とするのです. この仕組みで
0 を中心に対称になるように正負の数を扱おうとすると,
次のようになります.