実習 2: $1 - 1/2 + 1/3 - \cdots$

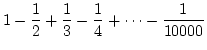次は, $${ 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4} +\cdots - \frac{1}{10000}}$$ を計算します. この和を大きい方からと, 小さい方から の 2通りで計算してみます. 丸め誤差の積み重ねを実感して頂くためで, 『塵も積もれば山となる』の実例です.

プログラムの先頭の方にある #define TERMNUM 10000 は, cpp (C preprocessor) に対する指示で, プログラムソースの中にある TERMNUM という文字列を 10000 に置き換えるという意味になります. また, sign/((double) i) という部分がありますが, これは異なる 型の変数の割算をする際に, int 型 i を double 型に変換して割算を 実行させるためです. C 言語の仕様の上では, 異なる型の計算は自動的に 範囲の大きい方に合わせて実行されますが, 敢えて明示的に型変換を 記述しました. このような型変換を変数のキャスト(cast)といいます.

/* File name 5-4.c */

#include <stdio.h>

#define TERMNUM 10000
main()
{
       int i;
       double sign=1.0;
       double sum1=0.0;
       double sum2=0.0;

       for(i=1; i <= TERMNUM; i++){
              sum1= sum1+sign/((double) i);
              sign*=-1.0;
       }
       sign=-1.0;

       for(i=TERMNUM; i >= 1; i--){
              sum2= sum2+sign/((double) i);
              sign*=-1.0;
       }       

       printf("sum1 = %18.17f, sum2 = %18.17f\n",sum1, sum2);
}

プログラムを実行してみるとわかりますが. 計算方法 によって答が違います. ちなみに和の正確な値は, 0.693097183059945296917232371458 で, 小さい方からの和の方が, 3桁程精度が良くなります.

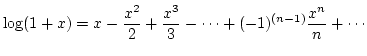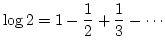良く知られているように,$\vert x\vert < 1$ の領域で, $${\log (1+x) = x - \frac{x^2}{2}+ \frac{x^3}{3} - \cdots + (-1)^{(n-1)}\frac{x^n}{n} + \cdots}$$ が成立します. この級数は $x=1$ でも収束し $${\log 2 = 1 - \frac{1}{2} + \frac{1}{3} - \cdots}$$ が成立します.(練習問題 1) $\log 2 =0.69314718055994530942$ ですから, 上の和の収束はとても遅く, これを使って $\log 2$ を計算するのは 得策ではありません.