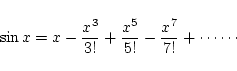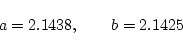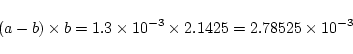Next: 練習問題
Up: 近似値と誤差
Previous: 誤差の限界
コンピュータや電卓では, 入力された10進数は内部で2進数に変換されて,
計算などの処理が行われてます. 2進数でも, 10進数の場合と同様に小数が
考えられ, 2進数の101.011とは,
と表される数のことであり, 10進数で表すと 5.375 です.
10進数の有限小数は, 2進数に変換すると無限小数になる場合があります.
例えば, 10進数の小数0.1を2進数に変換すると
と, 無限小数になります.
コンピュータや電卓には, 0と1を記憶する場所がたくさんありますが, 無限
ではなく有限です. そのため, 上のような無限小数は, 何桁目かで切り捨てや
切り上げなどの, いわゆる「丸める」操作が施された有限小数として記憶されます.
また,計算の途中に現れる数値にも,「丸める」操作がしばしば施されます.
このような操作のために生じる誤差を, 丸め誤差といいます.
例えば, 電卓で(1
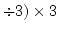 の計算を行うとき, 丸め誤差のために,
正しい答 1ではなく, 0.9999...と表示されることが普通です.
の計算を行うとき, 丸め誤差のために,
正しい答 1ではなく, 0.9999...と表示されることが普通です.
コンピュータは, 非常に多い回数の計算を高速で行いますが, 無限回の計算を
するわけではありません. 弧度法で表された角 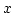 の三角関数
の三角関数 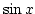 は
は
と, 項が無限に続く式になります.
この式を用いてコンピュータで 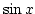 の値を求める場合,
無限回の計算は行えないので, 右辺を有限個の項で打ち切って,
その近似値を求めることになります. このような事情のために生じる誤差を,
打ち切り誤差といいます.
の値を求める場合,
無限回の計算は行えないので, 右辺を有限個の項で打ち切って,
その近似値を求めることになります. このような事情のために生じる誤差を,
打ち切り誤差といいます.
コンピュータを利用するときに生じる上のような誤差のほかに, 有効数字の極端な
桁落ちによる誤差もあります. 例えば,有効数字が5桁の非常に近い2つの数
の差は
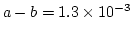 となり, 有効数字が2桁に落ちます. そのため,
この差にbを掛けた
となり, 有効数字が2桁に落ちます. そのため,
この差にbを掛けた
では, 有効数字は最初の2つだけになり, 結果は
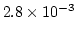 と
すべきです. 即ち, 相対誤差が, 拡大された事になります.
と
すべきです. 即ち, 相対誤差が, 拡大された事になります.
以上のような誤差は, 1回の計算では微小であっても, 例えば,
コンピュータが得意とする繰り返し計算などでは, 計算回数が多くなるに
従って誤差が累積し, 無視できなくなる可能性が多くあります.
Next: 練習問題
Up: 近似値と誤差
Previous: 誤差の限界
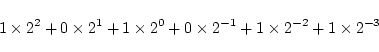
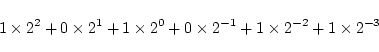
![]() の三角関数
の三角関数 ![]() は
は