


Next: クイックソートのライブラリ
Up: クイックソート(quick sort)
Previous: クイックソート(quick sort)
整列したい配列を, a[0], a[1], 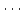 , a[n] とします. 整列は,
添字 0, 1,
, a[n] とします. 整列は,
添字 0, 1, 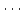 , n をつけ替えて, 小さい順にデータが並ぶよう
にする事で実現します. クイックソートのアルゴリズムは,
次のようになります.
, n をつけ替えて, 小さい順にデータが並ぶよう
にする事で実現します. クイックソートのアルゴリズムは,
次のようになります.
- 適当にひとつの値 a[k] を選ぶ. a[k] を pivot(ピボット, 軸)といいます.
- a[0], a[1],
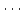 , a[n] の番号をつけ替えて,
a[0],
, a[n] の番号をつけ替えて,
a[0], 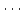 , a[i-1] は a[k] 以下の値を持ち,
a[i](i 番目)に 上の a[k] を入れ, a[i+1],
, a[i-1] は a[k] 以下の値を持ち,
a[i](i 番目)に 上の a[k] を入れ, a[i+1], 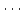 , a[n]
は a[k] より大きい値が入るようにする. (通常は k と i は
異なる値になる)
, a[n]
は a[k] より大きい値が入るようにする. (通常は k と i は
異なる値になる)
- 二つの配列 a[0],
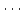 , a[i-1] と a[i+1],
, a[i-1] と a[i+1], 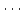 a[n] に対し, 上と同じ操作を(即ちクイックソート)を行う.
ただし, 配列の大きさが 1 であれば何もしない.
a[n] に対し, 上と同じ操作を(即ちクイックソート)を行う.
ただし, 配列の大きさが 1 であれば何もしない.
上の操作では, 一回のステップで必ずソートする配列のサイズが小さく
なっていますから, いつかは処理が終ります. また, 処理が終った時点で
整列が完成している事は明らかです.
この様に, 問題をより小さい集合の問題に帰着させて解くやり方を,
分割統治法(divide and rule または divide and conquer)
といいます.
クイックソートの着目点は, 集合を分けるところです. 一回のステップで
上手に集合を分割できれば, 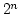 の分割動作が起こる事になり, これが
処理速度の速さの理由です. 即ち, 処理速度は着目するピボットの
取り方がクイックソートの処理速度を決めます. データの量が多くなると,
ピボットは配列する集合の平均値に近い値を取るようにしますが,
少ないと逆に平均値に近い値を取るという処理が無視できなくなります.
の分割動作が起こる事になり, これが
処理速度の速さの理由です. 即ち, 処理速度は着目するピボットの
取り方がクイックソートの処理速度を決めます. データの量が多くなると,
ピボットは配列する集合の平均値に近い値を取るようにしますが,
少ないと逆に平均値に近い値を取るという処理が無視できなくなります.
クイックソートの平均的な計算量は 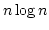 です.
ここで
です.
ここで 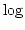 は自然対数ではなく, 2を底とする対数です.
計算量の世界では, 冪乗や対数の底は 2を利用するのが普通です.
また, 上はあくまでも平均的な計算量で, 最悪の計算量は
クイックソートでも
は自然対数ではなく, 2を底とする対数です.
計算量の世界では, 冪乗や対数の底は 2を利用するのが普通です.
また, 上はあくまでも平均的な計算量で, 最悪の計算量は
クイックソートでも 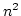 のオーダーになります.
のオーダーになります.
Next: クイックソートのライブラリ
Up: クイックソート(quick sort)
Previous: クイックソート(quick sort)
![]() の分割動作が起こる事になり, これが
処理速度の速さの理由です. 即ち, 処理速度は着目するピボットの
取り方がクイックソートの処理速度を決めます. データの量が多くなると,
ピボットは配列する集合の平均値に近い値を取るようにしますが,
少ないと逆に平均値に近い値を取るという処理が無視できなくなります.
の分割動作が起こる事になり, これが
処理速度の速さの理由です. 即ち, 処理速度は着目するピボットの
取り方がクイックソートの処理速度を決めます. データの量が多くなると,
ピボットは配列する集合の平均値に近い値を取るようにしますが,
少ないと逆に平均値に近い値を取るという処理が無視できなくなります.
![]() です.
ここで
です.
ここで ![]() は自然対数ではなく, 2を底とする対数です.
計算量の世界では, 冪乗や対数の底は 2を利用するのが普通です.
また, 上はあくまでも平均的な計算量で, 最悪の計算量は
クイックソートでも
は自然対数ではなく, 2を底とする対数です.
計算量の世界では, 冪乗や対数の底は 2を利用するのが普通です.
また, 上はあくまでも平均的な計算量で, 最悪の計算量は
クイックソートでも ![]() のオーダーになります.
のオーダーになります.