- 下の処理を
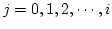 の間繰り返す.
の間繰り返す.
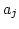 と
と 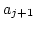 を比較し,
を比較し,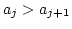 ならば,
これを入れ替える. そうでなければ, 何もしない.
ならば,
これを入れ替える. そうでなければ, 何もしない.
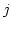 を 1つ進める.
を 1つ進める.
バブルソートでは, 外側の i のループが n回実行され, 内側の j のループで
値の入れ換えが, 平均 n/2 回 実行されます. 従って,
計算量はおよそ, ![]() となります. 計算量を問題にするときには,
定数倍は無視して, n の冪乗部分だけを問題にします.
バブルソートの計算量は, 「
となります. 計算量を問題にするときには,
定数倍は無視して, n の冪乗部分だけを問題にします.
バブルソートの計算量は, 「![]() のオーダー」であるといいます.
実際の問題では, これでは効率が悪く, バブルソートを利用する事は
ほとんどありません. ただし, アルゴリズムがわかりやすく
記述が簡単ですから, ちょっとしたプログラムには, 使えなくはありません.
バグの無いプログラムが書きやすいというのは, 1つの利点です.
のオーダー」であるといいます.
実際の問題では, これでは効率が悪く, バブルソートを利用する事は
ほとんどありません. ただし, アルゴリズムがわかりやすく
記述が簡単ですから, ちょっとしたプログラムには, 使えなくはありません.
バグの無いプログラムが書きやすいというのは, 1つの利点です.
今回のプログラムは全て整列するプログラムが同じで, main() の前にある
int data[SIZE]= {99,73,20,32,34,5,64,97,25,12,83,9,21,40,3,44,69,15,58,75};
という配列であるとします.
次のプログラムは, バブルソートのアルゴリズムを C で記述してみた ものです. ペイジがまたがっていますが, 我慢して下さい.
/* File name 13-1.c */
#include <stdio.h>
#define SIZE 20
int data[SIZE]= {99,73,20,32,34,5,64,97,25,12,83,9,21,40,3,44,69,15,58,75};
main()
{
int i, j;
int temp;
for (i=SIZE-1 ; i > 0; i--){ /* Sort Process */
for (j=0; j < i; j++){
if (data[j] > data[j+1]){
temp = data[j+1];
data[j+1]=data[j];
data[j]=temp;
}
}
} /* End of sorting. */
for( i=0; i< SIZE; i++) /* Output the result. */
printf("%d ", data[i]);
printf("\n");
}