プログラムを書くときの考え方

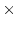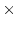実際にプログラムを書く時には, 上のアルゴリズムをもう少し具体的に する必要があります. ここでは簡単のために, 4$\times$ 4 行列の逆行列 を扱う事とし, アルゴリズムを見やすくするために, 逆行列を求めるのに 必要な 4$\times$8 行列は大域変数で定義します. 大域変数は, プログラムの中のどの函数でも, その値を参照し 変更する事が出来ます. 従って, 函数は全て void 型で, 各函数から直接 大域変数の値を変更しています. ただし, 大域変数による副作用もあります. 上にも述べましたが, いつでも値が変えられるのは, 値の変化を追うのが 難しくなり, プログラムの間違いの発見が大変になります.(基本的に, 最初は間違ったプログラムを書いてしまい, それを正しく動作するように 変更して行くのが実際のプログラミングです.) その意味で, 実践的なプログラミングでは, 大域変数はできる限り使わないようにします.

数値計算上, pivot はその列の絶対値の最大値を取ります. 0に近い値を取ってしまうと, その数での割算が, 誤差の拡大につながるからです. しかしここでは, 簡単のために, その列で 0 でない最初の数とします.

これらの事を考慮すると, 次のような操作がプログラムの全体となります.

1. 行列を入力する.
2. 逆行列を計算する.
   最初の列から順に各列ごとに
   1. pivot を定める.
      1. 対角成分が 0 でなければそれが pivot
      2. そうでなければその列を下に見て, 成分が 0 でない行と交換
         もしそのような成分が見つからなければ, 逆行列を持たない.
   2. 掃き出しを実行する.
      1. 列と同じ番号の行を対角成分で割る.
      2. 最初の行から順に残りの行を掃き出す.
3. 結果を出力する.

このようにして実際に書いたのが, 次のセクション全体です. プログラムの中では行列を表すのに 2次元の配列が用いられています. また, 2次元配列の初期化の方の方法も, これでわかると思います.