


Next: プログラムを書くときの考え方
Up: 計算機言語 I 第 11
Previous: 大域変数と局所変数
よく知られているように, 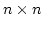 行列は行列式が 0 でないとき
逆行列を持ちます. 逆行列は Cramer の公式によって与える事ができます.
線形代数学の授業でも学んだと思いますが, Cramer の公式は数学の理論を
作るには重要ですが(数学だけではなく電気工学などでも, 理論上は重要),
与えられた逆行列の計算には向きません.
多量の行列式の計算が大変だからです.
行列は行列式が 0 でないとき
逆行列を持ちます. 逆行列は Cramer の公式によって与える事ができます.
線形代数学の授業でも学んだと思いますが, Cramer の公式は数学の理論を
作るには重要ですが(数学だけではなく電気工学などでも, 理論上は重要),
与えられた逆行列の計算には向きません.
多量の行列式の計算が大変だからです.
その事情はプログラミングでも同じで, 逆行列の計算をプログラム
する際にも, Cramer の公式は使いません. プログラム
されるのは Gauss の消去法(掃き出し法)です. 即ち, 中学で学ぶ連立
方程式の解法です.
掃き出し法は, 次のアルゴリズムです.
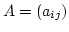 を
を 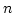 次正方行列とします.
次正方行列とします. 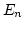 を
を 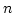 次の単位
行列とする時,
次の単位
行列とする時, 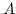 と
と 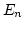 を横に並べてできる
を横に並べてできる
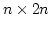 行列
行列 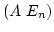 を考えます. これに対して行の
基本変形, 即ち
を考えます. これに対して行の
基本変形, 即ち
- ある行を(0 でない)定数倍する.
- ふたつの行を入れ換える.
- ある行に, 別の行の定数倍を加える.
を実行して, 左半分の 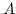 の部分を単位行列に変形し,
の部分を単位行列に変形し,
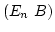 の形にできたとします. このとき,
の形にできたとします. このとき, 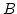 は
は 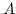 の逆行列です.
もし,
の逆行列です.
もし, 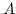 を単位行列に変形できなければ,
を単位行列に変形できなければ, 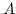 は逆行列を持ちません.
は逆行列を持ちません.
より具体的なアルゴリズムは, 次の形になります.
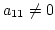 かどうかを調べる. もし
かどうかを調べる. もし 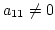 なら3に進む.
なら3に進む.
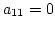 なら列を下に見て, すなわち
なら列を下に見て, すなわち
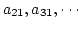 で 0 でないのものを捜し出して, その行と1行を入れ換える.
で 0 でないのものを捜し出して, その行と1行を入れ換える.
- 第 1 行を
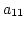 でわる.
でわる.
- 第
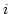 行
行 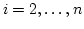 から 3 でできた 第1行の
から 3 でできた 第1行の 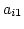 倍を引く.
倍を引く.
この操作で
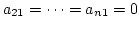 となる.
となる.
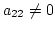 かどうかを調べる. もし
かどうかを調べる. もし 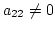 なら7に進む.
なら7に進む.
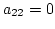 なら列を下に見て, すなわち
なら列を下に見て, すなわち
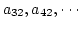 で 0 でないのものを捜し出して, その行と2行を入れ換える.
で 0 でないのものを捜し出して, その行と2行を入れ換える.
- 第 2 行を
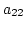 でわる.
でわる.
- 第
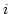 行
行
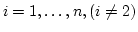 から 7 でできた 第2行の
から 7 でできた 第2行の 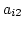 倍を引く.
倍を引く.
この操作で
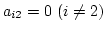 となる.
となる.
- 以下同様の操作を第
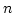 列まで繰り返す.
列まで繰り返す.
すなわち, 各列毎に対角成分に 0 でない値を選んで来て,
それを利用して, その列の他の成分を消去して行くわけです.
この 0 でない値の事を, pivot(軸)といいます. pivot を選べなくなった時点
でこのアルゴリズムは止まってしまい, その場合には
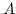 が逆行列を持ちません.
が逆行列を持ちません.
Next: プログラムを書くときの考え方
Up: 計算機言語 I 第 11
Previous: 大域変数と局所変数
![]() を
を ![]() 次正方行列とします.
次正方行列とします. ![]() を
を ![]() 次の単位
行列とする時,
次の単位
行列とする時, ![]() と
と ![]() を横に並べてできる
を横に並べてできる
![]() 行列
行列 ![]() を考えます. これに対して行の
基本変形, 即ち
を考えます. これに対して行の
基本変形, 即ち
![]() が逆行列を持ちません.
が逆行列を持ちません.