打ちきり誤差

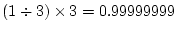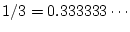これは, コンピュータがディジタルである事に由来します. 例えば 電卓の計算で, $(1\div 3) \times 3 = 0.99999999$ となって, 正確な 値がでて来ない事は, 良くご存知だと思います. これは, $1/3 = 0.333333\cdots$ が無限小数になるのに対して, 電卓では 有限桁で切捨てを実行するからです.

これと同じ事が, コンピュータを使った 2進法の計算でも起きます. ただし, 打ちきり誤差の現れ方は, 2進法と10進法では異なります. これらのことへの対処は, 次の方法を取ります.

1. 科学技術計算の場合: あらかじめ起こり得る誤差を計算しておき, 誤差が実用範囲内に収まる事をチェックしておく, あるいは計算を繰り返す 事により, 誤差が影響を与えない様なアルゴリズムを用いるのが最善です. しかし, 簡単な計算に於いても誤差の影響ははかり知れない ような実例もあります(カオスと呼ばれる現象).
2. 金融関連の計算の場合: お金関連の計算や, 電卓をプログラム で作る場合などは, 打ちきり誤差の現れ方を, 10進法の計算に合う ようにプログラムを工夫をすることがあります. 即ち, 電卓と同じ計算が 起こるようにします. ただし, この方法に関しては, この講義では触れません.