Next: コンピュータ内のデータその 2, 文字コード: 例として, Up: コンピュータはどのような構成になっているか Previous: ハードウェアとソフトウェア
まず, 一般的な数の表記 (記数法) について述べます
2.
通常, 数は789.012のように書かれます. この意味は,
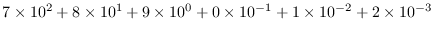 の 10 のベキ乗の係数を順に並べて書いたもので,
10進法表記と言います. 10のことをこの表記の基数と言います.
10 進法表記では, 数を表すのに 0 – 9 の 10個の文字を用います.
10 を基数とするのは, ヒトの両手の指の総数が 10 本であるからだと考えられていますが,
数学的に合理的である事が証明されている訳ではないと思います.
ヨーロッパ系言語の数詞を見ますと, 必ずしも言葉は 10進法ではありません.
従って, 10進法は歴史的には割に新しい数の表記法です.
の 10 のベキ乗の係数を順に並べて書いたもので,
10進法表記と言います. 10のことをこの表記の基数と言います.
10 進法表記では, 数を表すのに 0 – 9 の 10個の文字を用います.
10 を基数とするのは, ヒトの両手の指の総数が 10 本であるからだと考えられていますが,
数学的に合理的である事が証明されている訳ではないと思います.
ヨーロッパ系言語の数詞を見ますと, 必ずしも言葉は 10進法ではありません.
従って, 10進法は歴史的には割に新しい数の表記法です.
基数を 10 にするのは人間的な都合ですが, 10以外の基数であっても,
上のような数の表記は, 筆算が可能であると言う意味では合理的です.
例えば, ローマ数字を用いたかけ算を考えると, 実行がとても難しい事は,
ちょっとやればわかります (ローマ数字については, 各自調べて下さい).
上の基数を 2に変えたものが, 2進法です
3. 2 進法では,
数を表すのに 0, 1 の 2 つの文字しか用いません.
2進法で 101.011 は,
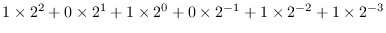 の意味で, これを 10進法で書くと 5.375 になります.
の意味で, これを 10進法で書くと 5.375 になります.
コンピュータの世界では 2 進法は自然なのですが,
人間に取っては小さい数を表すのにも多量の桁数を必要とするため,
双方で便利な記法として 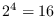 を基数とする 16進法もよく用いられます
4.
この場合, 数を表記するのに 16個の文字が必要となりますが,
数字としては存在しないので, A, B, C, D, E, F
(もしくは, a, b, c, d, e, f)をそれぞれ 10進法の
10, 11, 12, 13, 14, 15 を表す文字として用います.
を基数とする 16進法もよく用いられます
4.
この場合, 数を表記するのに 16個の文字が必要となりますが,
数字としては存在しないので, A, B, C, D, E, F
(もしくは, a, b, c, d, e, f)をそれぞれ 10進法の
10, 11, 12, 13, 14, 15 を表す文字として用います.
もう 1 つ, (数学ではあまり現れませんが)浮動小数点表記というものがあります.
化学で習ったアボガドロ数
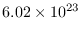 や物理で習った電気素量
(電子 1 個の電荷)
や物理で習った電気素量
(電子 1 個の電荷)
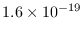 クーロンです. これらは,
人間の普段の暮らしからすると大きすぎたり, (絶対値が)小さすぎたりする値で,
表記の桁数を少なくするために, 上の様に数桁の有効数字に
10のベキ乗を掛けた形で書かれます. このような表記の仕方を,
浮動小数点数(浮動小数点表記)と言います. 左側にある有効数字の部分を仮数部,
右側にある 10のベキの部分を指数部と言います.
クーロンです. これらは,
人間の普段の暮らしからすると大きすぎたり, (絶対値が)小さすぎたりする値で,
表記の桁数を少なくするために, 上の様に数桁の有効数字に
10のベキ乗を掛けた形で書かれます. このような表記の仕方を,
浮動小数点数(浮動小数点表記)と言います. 左側にある有効数字の部分を仮数部,
右側にある 10のベキの部分を指数部と言います.
コンピュータでも浮動小数点数の計算は可能であり, 上の例では 10進法で表記していますが, コンピュータでの実際の計算では, 仮数部, 指数部共に 2を基数とする数に変換されて計算されます. 通常の数, 浮動小数点数ともに, コンピュータの中にあるのは有限桁数の数であり, 数学のような理想的な整数や実数が計算機で実現できている訳ではありません. ただし, 普段の人間の実用に必要な範囲での数の世界は, 実現されていると言って良いでしょう.
2024-04-26