Next: フリーソフト(Free software)を利用するときの注意 Up: 補足 Previous: 統計と社会
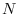 個のデータ
個のデータ
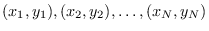 が与えられたとき,
が与えられたとき,
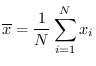 ,
,
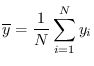 をそれぞれの平均値とすると,
をそれぞれの平均値とすると,
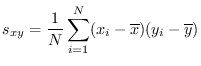 を共分散と言います.
を共分散と言います.
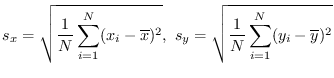 をそれぞれ
データ
をそれぞれ
データ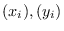 の標準偏差と言います. このとき相関係数は
の標準偏差と言います. このとき相関係数は
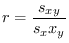 で定義されます.
で定義されます.
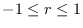 が証明され,
データ
が証明され,
データ 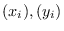 に関係がありそうか否かの数値的な指標になります.
に関係がありそうか否かの数値的な指標になります.
注意してほしいのは, 相関関係と因果関係を混同しないことです. 二つの指標に相関が認められても, その二つは全く無関係であることが 普通にあります(疑似相関).
SUGA Shuichi