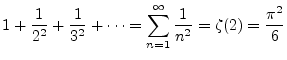 も次で計算させると, 円周率を使った答が出ます.
も次で計算させると, 円周率を使った答が出ます.
数式処理に欠かせない定数(円周率等)が既に定義されています. 円周率は, Piという記号を使います.
> Pi; > cos(Pi/4); > tan(Pi/2); > arctan(-infinity);
Maple では, 有理数, 冪根, 円周率等の定数は, そのまま出力されます.
上の逆正接函数の計算でもそうですし,
例えば,
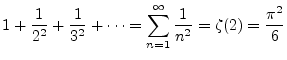 も次で計算させると, 円周率を使った答が出ます.
も次で計算させると, 円周率を使った答が出ます.
> sum(1/n^2, n=1..infinity);これを小数へ変換するには, evalfという手続きを用います.
> evalf(Pi^2/6);
Maple では, 非常に正確な数値計算ができます.
例えば,
![]() を C言語付属の
数学関数ライブラリで計算しますと -480 という答を得ますが, Maple を
使うと, C言語の計算がとんでもない誤差を含んでいる事がわかります.
起動時のデフォルトでは, 浮動小数点の仮数部は10桁に設定されており,
そのままで計算しますと, この結果は真の値の約40倍という, やはり
とんでもない答が返って来ますので, 仮数部の桁数を事前に設定します.
仮数部の桁数は, Maple のシステム変数 Digits に格納されていますから,
この値を変更します. Maple では代入には := を用います.
を C言語付属の
数学関数ライブラリで計算しますと -480 という答を得ますが, Maple を
使うと, C言語の計算がとんでもない誤差を含んでいる事がわかります.
起動時のデフォルトでは, 浮動小数点の仮数部は10桁に設定されており,
そのままで計算しますと, この結果は真の値の約40倍という, やはり
とんでもない答が返って来ますので, 仮数部の桁数を事前に設定します.
仮数部の桁数は, Maple のシステム変数 Digits に格納されていますから,
この値を変更します. Maple では代入には := を用います.
> Digits:=50; > evalf(exp(Pi*sqrt(163))-744-640320^3);C言語のライブラリを用いた計算が, 真の値の
文字式の展開, 因数分解も可能です.
> expand((x+y)^5); > factor(a^8-b^8);
次の問題は, 2000年の琉球大学入学試験問題前期日程数学甲の![]() です.
です.
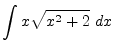 を求めよ.
を求めよ.
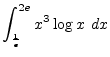 を求めよ.
を求めよ.
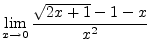 を求めよ.
を求めよ.
> diff(x/sqrt(1+x^2),x); > simplify(%); > int(x*sqrt(x^2+2),x); > int(x^3*log(x), x=exp(-1)..2*exp(1)); > limit((sqrt(2*x+1)-1-x)/x^2, x=0);
方程式 ![]() の解を求める様々な方法も Maple には用意されています.
の解を求める様々な方法も Maple には用意されています.
![]() が 4次以下の多項式なら, この方程式には
代数的な解法が存在する事が知られています.
(3年の代数学 I・II で勉強する予定です.)
Maple はこれらの解法を知っており, solve という手続きに
なっています. 次を実行してみて下さい.
これらの解には複素数が含まれますが, Maple では虚数単位は大文字の
I で表示されます.
が 4次以下の多項式なら, この方程式には
代数的な解法が存在する事が知られています.
(3年の代数学 I・II で勉強する予定です.)
Maple はこれらの解法を知っており, solve という手続きに
なっています. 次を実行してみて下さい.
これらの解には複素数が含まれますが, Maple では虚数単位は大文字の
I で表示されます.
> solve(x^3+1,x); > solve(x^3+3*x+1,x);
5次以上の方程式には, 代数的な解法が一般には存在しない事が 知られています. (代数的という制限を外せば, 別な解法はあります.) 次を実行してみてください.
> solve(x^5+x^2+1, x);RootOf(
代数的な解法がある場合でも, その解法が複雑な場合には, 残念ながら代数的な解を出力 しません. 例えば, 1の 7乗根を計算させようとしても, de Moivre の公式から出てくる解が単純に出力されるだけです.
> solve(x^7-1, x);上で述べたように Maple では, 代数的数が扱えます. これを利用すると,
> factor(x^6+x^5+x^4+x^3+x^2+x+1, (-7)^(1/2));従って, 1の複素7乗根は, 次の2つ方程式の解全体です.
> solve(2*x^3+x^2-I*sqrt(7)*x^2-x-I*sqrt(7)*x-2,x); > solve(2*x^3+x^2+I*sqrt(7)*x^2-x+I*sqrt(7)*x-2,x);
![]() が 5次以上の多項式や,
が 5次以上の多項式や, ![]() が多項式でない場合には, 一般的な
解法が存在しません.
このような方程式の近似解を数値的に計算する方法も Maple
は知っています. 上の方程式の数値解も, 次で計算してくれます.
が多項式でない場合には, 一般的な
解法が存在しません.
このような方程式の近似解を数値的に計算する方法も Maple
は知っています. 上の方程式の数値解も, 次で計算してくれます.
> fsolve(x^5+x^2+1, x);実際, 関数のグラフを描画する plot を使って,
> plot(x^5+x^2+1,x=-5..5); > plot(x^5+x^2+1,x=-2..0);等を実行しますと, fsolve で求めた値が