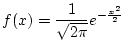 を -1.96 から 1.96 まで積分した値の近似値を
台形公式を用いて求めるプログラムを
作成せよ.(ヒント: 答は, 0.950 に近い)
分割の個数を 16, 128, 1024, 16384
とし, 0.950 との誤差を比較せよ.
を -1.96 から 1.96 まで積分した値の近似値を
台形公式を用いて求めるプログラムを
作成せよ.(ヒント: 答は, 0.950 に近い)
分割の個数を 16, 128, 1024, 16384
とし, 0.950 との誤差を比較せよ.
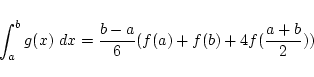
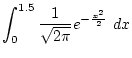 を区間を 65536等分してシンプソンの公式を用いて求めるプログラムを書け.
を区間を 65536等分してシンプソンの公式を用いて求めるプログラムを書け.
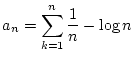 とおくとき,
とおくとき,
プログラムは, 丸め誤差ができる限り起こらないように工夫する事. ちなみに
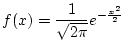 を -1.96 から 1.96 まで積分した値の近似値を
台形公式を用いて求めるプログラムを
作成せよ.(ヒント: 答は, 0.950 に近い)
分割の個数を 16, 128, 1024, 16384
とし, 0.950 との誤差を比較せよ.
を -1.96 から 1.96 まで積分した値の近似値を
台形公式を用いて求めるプログラムを
作成せよ.(ヒント: 答は, 0.950 に近い)
分割の個数を 16, 128, 1024, 16384
とし, 0.950 との誤差を比較せよ.
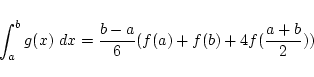
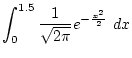 を区間を 65536等分してシンプソンの公式を用いて求めるプログラムを書け.
を区間を 65536等分してシンプソンの公式を用いて求めるプログラムを書け.
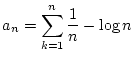 とおくとき,
とおくとき,