注意

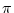1. $\pi$ の値は, /usr/include/math.h に M_PI で定義されています. このファイルには, 他にも様々な数学定数が定義されていますので, less で読んで 見て下さい.

2. 上の 2つの例とも分割の総数を 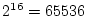$2^{16}=65536$ にしてあります. これは, コンピュータが 2進法の計算をするからで, こうしておくと 計算に誤差が現れにくいからです.

3. 台形公式が 1次函数, シンプソンの公式が 2次函数ですから, 3次函数, 4次函数 $\cdots$ と近似公式を作る事ができます. 次数をあげれば近似の精度 は, 一般的には上がりますが, 効果がどの程度かは, 菅は知りません.

4. 上のような, 有限区間で有界な滑らかな函数の数値積分では, シンプソンの公式の方が, 台形公式よりも一般的には良い近似を与えますが, 無限区間の積分や, 有界でない函数の積分の近似計算をする時には, 必ずしもこのことが成り立たないことが知られています. つまり, シンプソンの公式より, 台形公式の方が精度が良いという事が起こります.