定理の符号が異なるとき, すなわち,
ならば,
を満たす実数
が,
の間に少なくとも1つ存在する.
この定理を利用して, 方程式の近似解を求めるのが 2分法です.
関数 ![]() は, 区間
は, 区間 ![]() において連続で,
において連続で, ![]() を満たすとします.
また, 方程式
を満たすとします.
また, 方程式 ![]() はこの区間でただ 1つの解をもつと仮定します.
このとき, 区間
はこの区間でただ 1つの解をもつと仮定します.
このとき, 区間![]() の中点を
の中点を
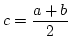 とすると
とすると
![]() の値は 0となるか, または
の値は 0となるか, または![]() のいずれかと異符号となります.
のいずれかと異符号となります.
ここで, ![]() なら
なら ![]() は方程式の解であり,
は方程式の解であり,
![]() なら, 方程式は区間
なら, 方程式は区間![]() に解をもち,
に解をもち,
![]() なら, 方程式は区間
なら, 方程式は区間![]() に解をもちます.
に解をもちます.
このように, 区間の中点を考えることにより,
解の存在する範囲を初めの半分に縮小することができます.
そして, この操作を繰り返すと,
誤差の限界を必要なだけ小さくした近似解が得られます.
double 型の計算機イプシロンが ![]() ですから,
52回くらい繰り返すと, 計算機の精度を越えます.
ですから,
52回くらい繰り返すと, 計算機の精度を越えます.
このようにして近似解を求める方法を2分法といいます.
一般に, 方程式 ![]() の近似解を, 誤差の限界が
の近似解を, 誤差の限界が ![]() として
2分法で求める手順は次のようになります.
として
2分法で求める手順は次のようになります.
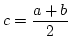 を求める.
を求める.
上の(3)において, ![]() のとき,
変数
のとき,
変数 ![]() の値をこのようにおき換えると,
の値をこのようにおき換えると, ![]() となり.
真の解
となり.
真の解 ![]() は区間
は区間 ![]() にあります.
またこのとき,
にあります.
またこのとき, ![]() の値は
の値は ![]() か
か ![]() に等しいから,
に等しいから,
![]() となり.
となり.
![]() を近似解としたときの誤差の限界は
を近似解としたときの誤差の限界は ![]() となります.
従って, (4)で誤差の限界が判定されます.
となります.
従って, (4)で誤差の限界が判定されます.
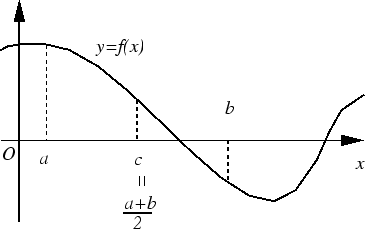
方程式 ![]() が区間
が区間 ![]() で3つの実数解
で3つの実数解
![]() をもち,
をもち,
![]() とする.
とする.
![]() を
を ![]() と
と ![]() の中点として 2分法を適用すると,
第 2段階以後区間
の中点として 2分法を適用すると,
第 2段階以後区間 ![]() は無視されて,
区間
は無視されて,
区間![]() にある解だけを近似することになります.
このように, ある区間で方程式が 2つ以上の解をもつ場合,
2分法で近似解を求めると, 1つの解以外は無視されます.
また, 例えば, 方程式
にある解だけを近似することになります.
このように, ある区間で方程式が 2つ以上の解をもつ場合,
2分法で近似解を求めると, 1つの解以外は無視されます.
また, 例えば, 方程式![]() の重解 1の近似値は, 2分法では求めることが
できません. 従って, 2分法を適用する場合, あらかじめ解について定性的に
調べておくことが必要です.
の重解 1の近似値は, 2分法では求めることが
できません. 従って, 2分法を適用する場合, あらかじめ解について定性的に
調べておくことが必要です.