


Next: レポート問題
Up: 計算機言語 I 第 4
Previous: 型に対する修飾語
-
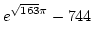 と
と 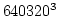 の差は,
幾らか ? その値を数学関数ライブラリを用いて計算するプログラムを書け.
(実際には
の差は,
幾らか ? その値を数学関数ライブラリを用いて計算するプログラムを書け.
(実際には
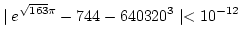 となる事が知られている. なぜ,
となる事が知られている. なぜ,
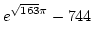 が整数の 3 乗に近いのか, その理由もできれば調べよ.)
が整数の 3 乗に近いのか, その理由もできれば調べよ.)
- Euler(オイラー)の関数
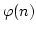 は, 2 以上の整数
は, 2 以上の整数 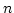 に対して,
1 から
に対して,
1 から 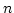 までの数で,
までの数で, 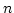 と互いに素な数の個数として定義される.
と互いに素な数の個数として定義される.
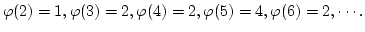 オイラーの関数を C 言語の関数として記述し,
オイラーの関数を C 言語の関数として記述し, 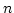 を入力した時その値を
出力するプログラムを書け.
を入力した時その値を
出力するプログラムを書け.
- 再帰を用いて Fibonacci 数列
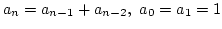 の第
の第 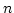 項を出力するプログラムを書け.
項を出力するプログラムを書け.
- 上のFibonacci 数列の一般項を求め, 数学関数ライブラリを用いて
第
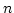 項を出力するプログラムを書け.
項を出力するプログラムを書け.
- 階乗
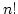 を再帰で求めるプログラムを書け.
を再帰で求めるプログラムを書け.
- さらに拡張して 2 項係数
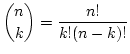 を求めるプログラムを書け.
を求めるプログラムを書け.
- 2項係数を漸化式
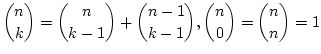 から再帰で計算するプログラムを書け.
から再帰で計算するプログラムを書け.
- 上の 2 つの 2 項係数のプログラム各々において,
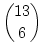 は, 正確な値が求まるか ? その理由は何故か ?
は, 正確な値が求まるか ? その理由は何故か ?
Subsections
Next: レポート問題
Up: 計算機言語 I 第 4
Previous: 型に対する修飾語
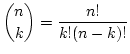 を求めるプログラムを書け.
を求めるプログラムを書け.
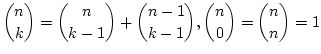 から再帰で計算するプログラムを書け.
から再帰で計算するプログラムを書け.
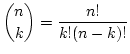 を求めるプログラムを書け.
を求めるプログラムを書け.
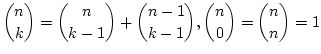 から再帰で計算するプログラムを書け.
から再帰で計算するプログラムを書け.