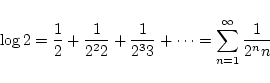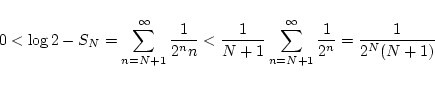Next: C言語のソースの清書(インデントをつける)
Up: 補足
Previous: 補足
以前に 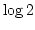 の値を精度を保証して計算せよという問題を出しましたが,
まだレポートとして受け取っていないので, ここでヒントを出します.
このような内容を書くべきか否かを迷いましたが, 最初の一歩は書いておいた
方が良いとの判断です.
の値を精度を保証して計算せよという問題を出しましたが,
まだレポートとして受け取っていないので, ここでヒントを出します.
このような内容を書くべきか否かを迷いましたが, 最初の一歩は書いておいた
方が良いとの判断です.
さて, 自然対数については, 次の Taylor 展開が 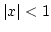 で成立します.
(
で成立します.
(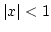 なら右辺の無限級数が収束して,
なら右辺の無限級数が収束して, 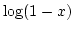 に一致する
という意味です. 詳しくは解析学 I で勉強して下さい.)
に一致する
という意味です. 詳しくは解析学 I で勉強して下さい.)
この式に
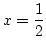 を代入しますと,
を代入しますと,
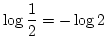 ですから,
ですから,
となります. この無限級数の第 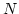 項までの部分和を
項までの部分和を 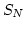 と
おくと,
と
おくと,
というふうに, 打ちきり誤差が評価されます. この評価を使って,
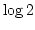 の近似計算ができます.
の近似計算ができます.
Next: C言語のソースの清書(インデントをつける)
Up: 補足
Previous: 補足
![]() で成立します.
(
で成立します.
(![]() なら右辺の無限級数が収束して,
なら右辺の無限級数が収束して, ![]() に一致する
という意味です. 詳しくは解析学 I で勉強して下さい.)
に一致する
という意味です. 詳しくは解析学 I で勉強して下さい.)
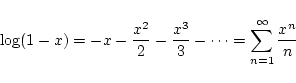
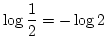 ですから,
ですから,